Projects
Variable Length Integer Encoding+
The IEEE 754 floating point standard is ubiquitous, however, it is rather inflexible due to a fixed-length exponent encoding and some additional drawbacks. Multiple new format families with variable length encoding of the exponent (tapered accuracy) have been suggested. But there are so many more possibilities, how do we know what is best? We develop a framework which allows the exploration of all options in variable-length integer encoding, i.e. all uniquely decipherable exhaustive binary codes can be represented.
Sparse Format Specialization+
The processing time of sparse representations of local discrete operators depends heavily on the storage format. The requirements of high accuracy, minimal memory footprint, high data locality, parallelism friendly layout, wide applicability, and easy modifiability are contradicting and therefore only case specific choices lead to satisfactory results.
Parallel Algebraic Multigrid Domain Decomposition+
★Parallel AMG-DD breaking the communication wall★ Algebraic Multigrid (AMG) has optimal computational complexity but the cost of communication limits its scalability on large clusters. Algebraic Multigrid Domain Decomposition (AMG-DD) is an algorithm that trades some additional computations for a significant reduction in communication cost, resulting in superior performance on communication limited systems with high local compute power (e.g. GPU-cluster).
Parallel Adaptive Data Structures+
While GPUs and other highly parallel devices excel in processing of regularly structured data their large SIMD width and high number of cores quickly leads to inefficiencies in fine-granular branches and complex synchronization. However, adaptive data structures that cause such problems are indispensable to capture multi-scale phenomena. We must rethink our data arrangement in order to reconcile parallel and adaptive requirements.
Graph Decompositions+
There are benefits in decomposing the adjacency graph of a sparse matrix into subgraphs. Depending on the decomposition we obtain better numerical schemes (e.g. better preconditioners) or better execution schemes (e.g. better data locality). However, we need fast parallel algorithms for the decompositions or else this preprocessing time eats up the benefits of the improved schemes.
Block Tridiagonal and Banded Linear Equation Systems+
★Scaled partial pivoting at maximum bandwidth★ These special cases of sparse systems appear often in practice, yet solving them in parallel with pivoting is very challenging because of problems with data dependent execution flow. Here we develop algorithms which implement the data dependent decisions without any SIMD divergence leading to far superior performance.
Algebraic Operator Splittings+
The main motivation behind operator splitting methods is the simpler and faster implicit treatment of individual components in comparison to the entire operator which is typically difficult to invert. We develop an algebraic framework for operator splitting preconditioners for general invertible sparse matrices. In particular, it generalizes ADI and ILU methods to multiple factors and more general factor form.
Parallel AMG, Krylov, multi-colored GS and ILU solvers+
★Comprehensive solver library for large GPU-clusters★ Algebraic multigrid is one of the main tools in science and industry for the solution of large sparse linear equation systems. The AmgX library executes AMG and Krylov methods with different preconditioners on GPU-systems with a single GPU, multiple GPUs and on GPU-clusters. Innovations in numerical schemes, graph algorithms and work scheduling enable the massively parallel execution.

Mixed-Precision Methods+
★Double accuracy with single precision GPUs and FPGAs★ To obtain a result of high accuracy it is not necessary to compute all intermediate results with high precision. Mixed precision methods apply high precision computations only where necessary and save space or time without decreasing the accuracy of the final solution.

Iterative Stencil Computations+
★Stencil algorithms breaking the memory wall★ Iterative stencil computations are ubiquitous in scientific computing and the exponential growth of cores in current processors leads to a bandwidth wall problem where limited off-chip bandwidth severely restricts their performance. In this project we aim at overcoming these problems by new algorithms that scale mainly with the aggregate cache bandwidth rather than the system bandwidth.
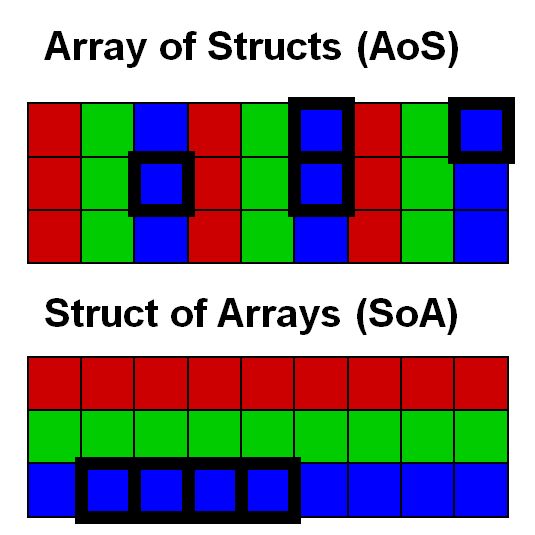
Data Layout Abstractions+
Data layout has tremendous impact on performance, in particular for high throughput devices. But traditional languages force the programmer to specify the memory layout of multi-valued data containers in a syntax that makes it impossible to change later without modifying all accesses to the data container. Data layout abstractions allow to switch between array of structs and struct of arrays layouts with a single parameter while keeping the traditional syntax.

Balanced Geometric Multigrid+
Neither solvers with best numerical convergence nor solvers with best parallel efficiency are the best choice for the fast solution of PDE problems in practice. The fastest solvers require a delicate balance between their numerical and hardware characteristics. Balancing both aspects we can even parallelize completely sequential preconditioners with large parallel speedup and hardly any loss in numerical performance.

GPGPU Scientific Computing
Scientific simulations have higher accuracy requirements than multimedia processing applications. With the introduction of optimized floating point processing units in graphics processors and reconfigurable hardware these devices are now also attractive as powerful scientific co-processors.

GPU-Cluster Computing
★Minimally invasive acceleration of legacy code on GPU-clusters★ A single GPU already offers two levels of parallelism, but similar to CPUs, demand for higher performance and larger problem sizes leads to the utilization of GPU-clusters, in which every cluster node is equipped with GPUs. This adds the intra-node and inter-node parallelism. The main challenge for these heterogeneous systems is the enormous discrepancy in the bandwidth between the two finer and two coarser levels of parallelism and their integration in legacy code.
GPGPU Geometric Refinement
GPUs process data of the same resolution very quickly with massive data parallel execution. But even the massive parallelism cannot compete with adaptive methods when the data size grows cubically under uniform refinement. This project develops parallel refinement strategies with grids and particles that allow to introduce higher resolution in only parts of the computational domain.
Visualization
The choice of visualization methods and parameters is already a part of the interpretation process of the data, as it emphasizes certain structures and subdues others. This can lead to positive effects uncovering otherwise unconceivable relations in the data, but may also produce false evidence. Combinations of multiple methods, and data based parameter controls try to limit this danger.
Reconfigurable Computing
This projects investigates how the enormous parallelism of reconfigurable hardware can be harnessed to accelerate PDE solvers. Both fine- and coarse-grained architectures are examined. The performance is very convincing but for complex problems higher level programming languages for these devices are required.
GPGPU Image Processing
★Pioneering work on PDE solvers with GPUs★ The data parallelism in typical image processing algorithms is very well suited for data-stream-based architectures. PDE based methods for image denoising, segmentation and registration have been thus accelerated on graphics cards.
GPGPU Computer Vision
Although graphics processor units (GPUs) are still very restricted in data handling some strategies allow the focusing of processing on data-dependent regions of interest. Thus computer vision algorithms which require computations on changing regions of interest can already benefit from the high GPU performance. Current implementations comprise the Generalized Hough Transform, skeleton computation and motion estimation.
